Finding Lottery Tickets in Vision Models via Data-driven Spectral Foresight Pruning

Abstract

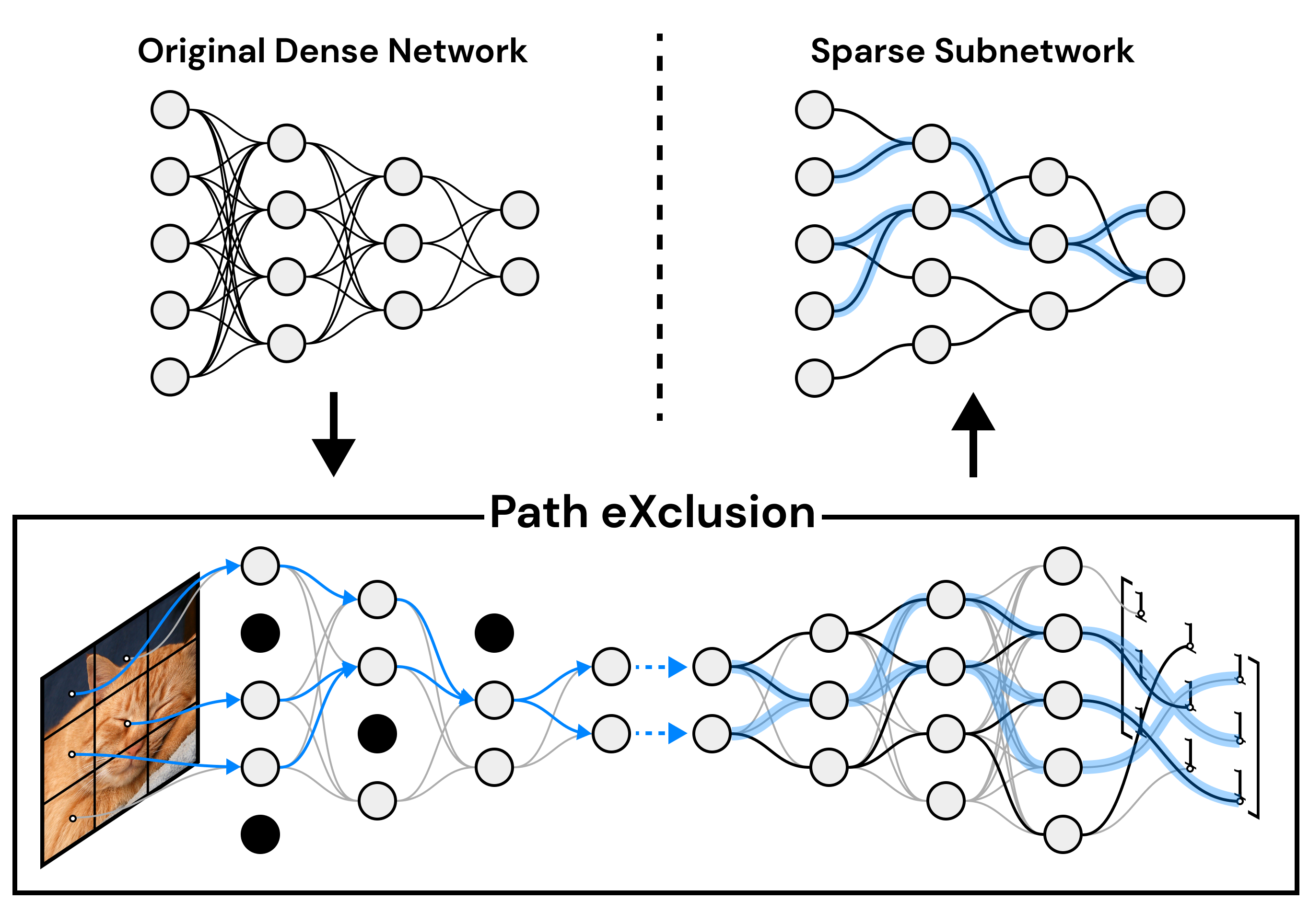
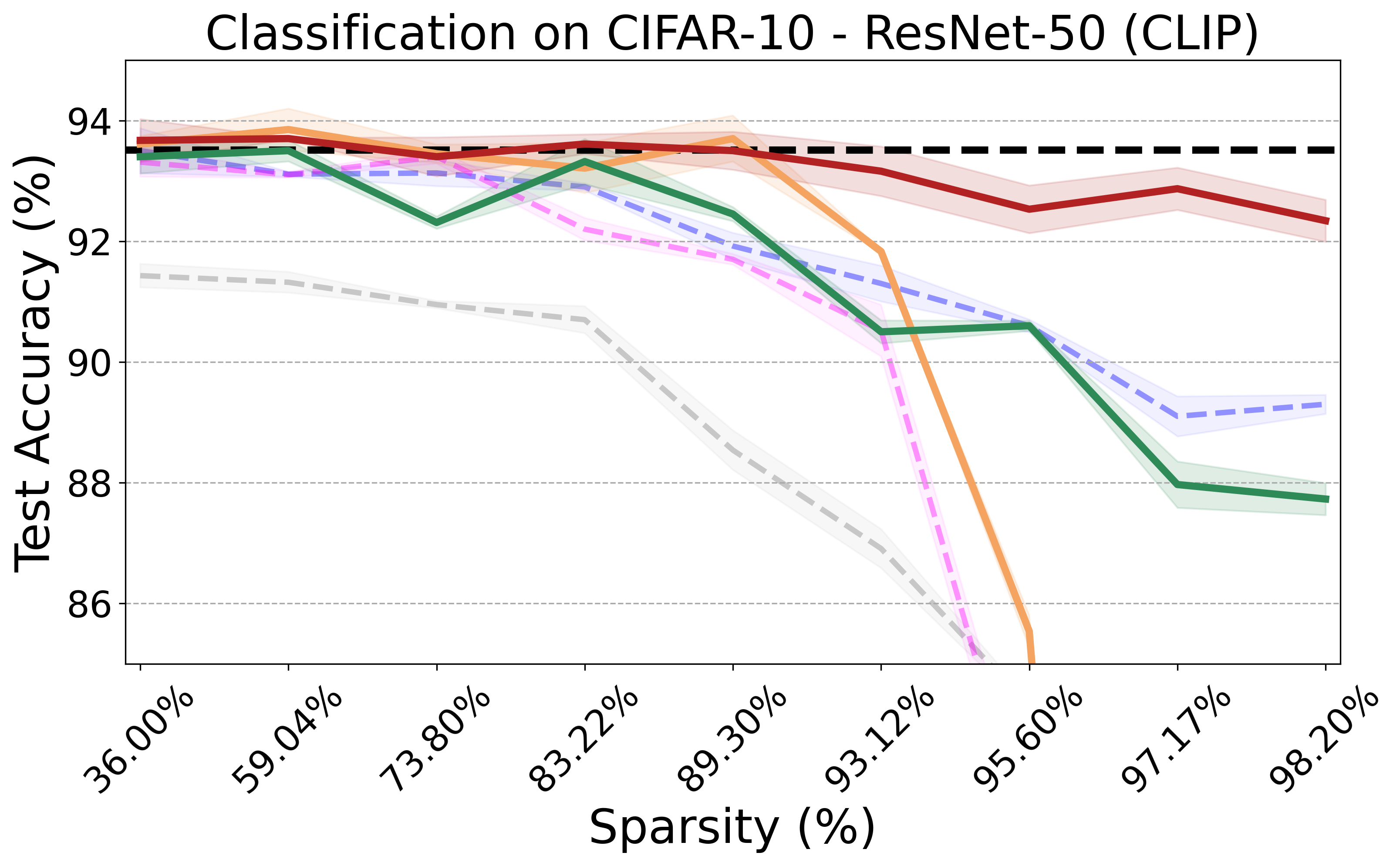
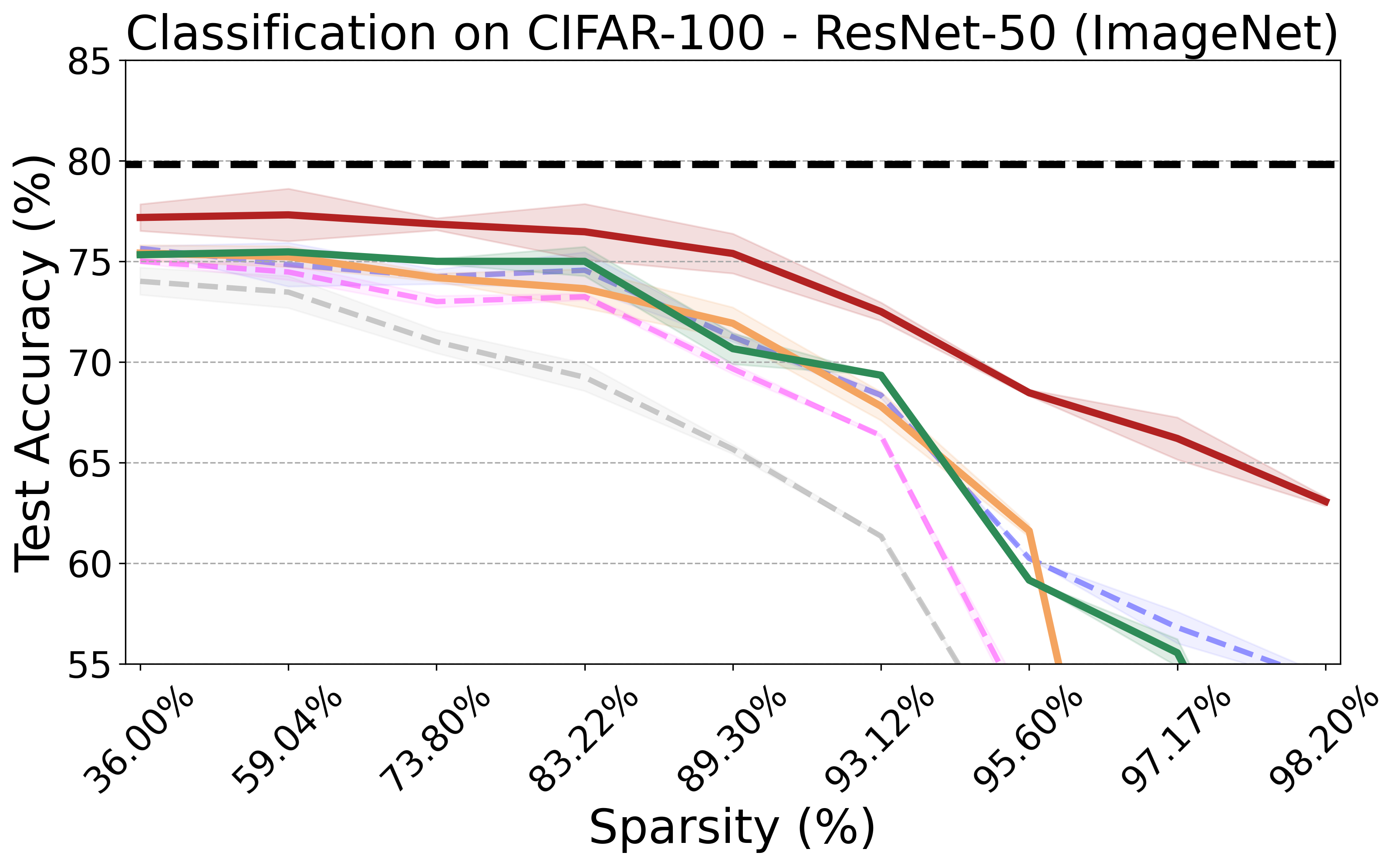
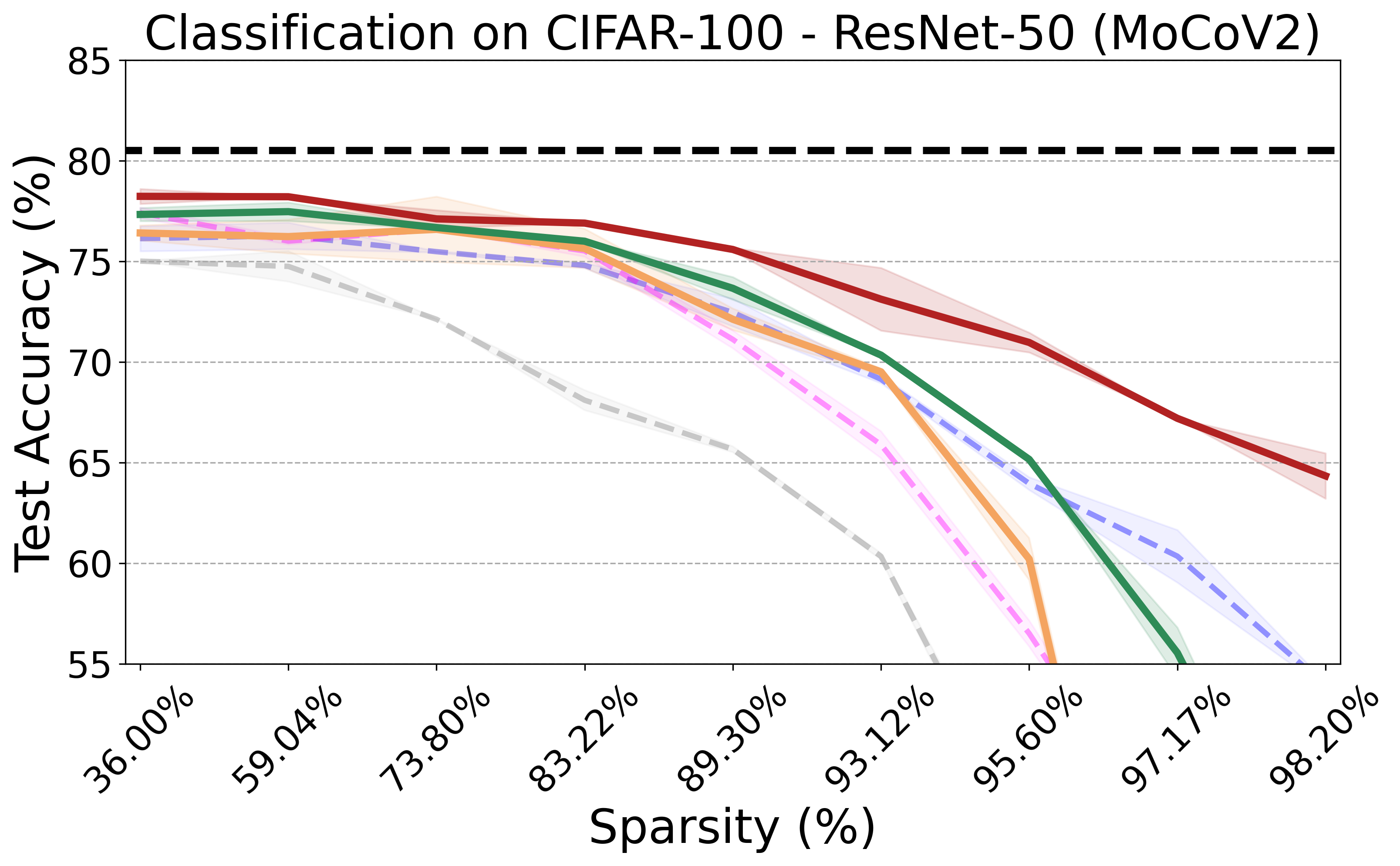
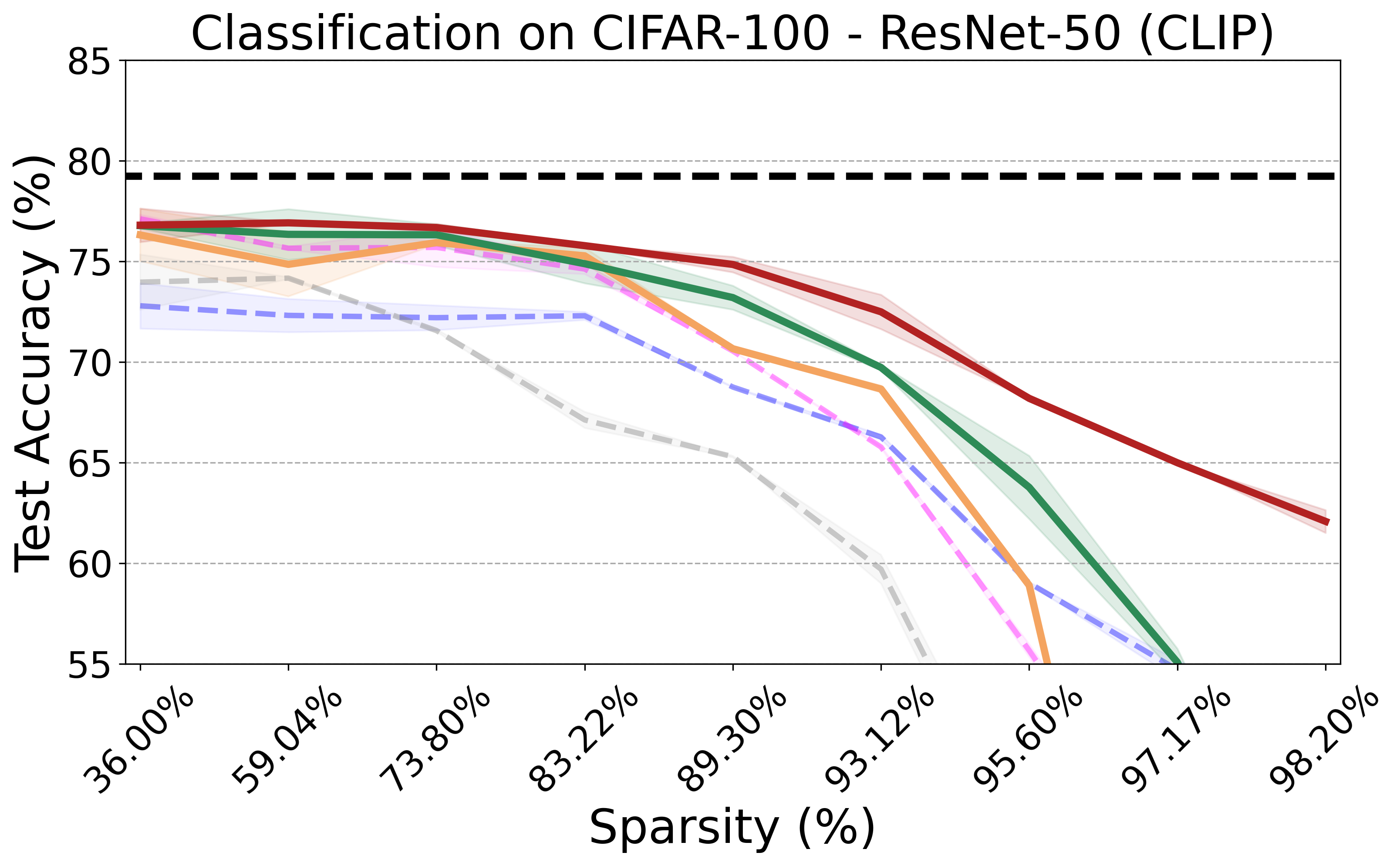
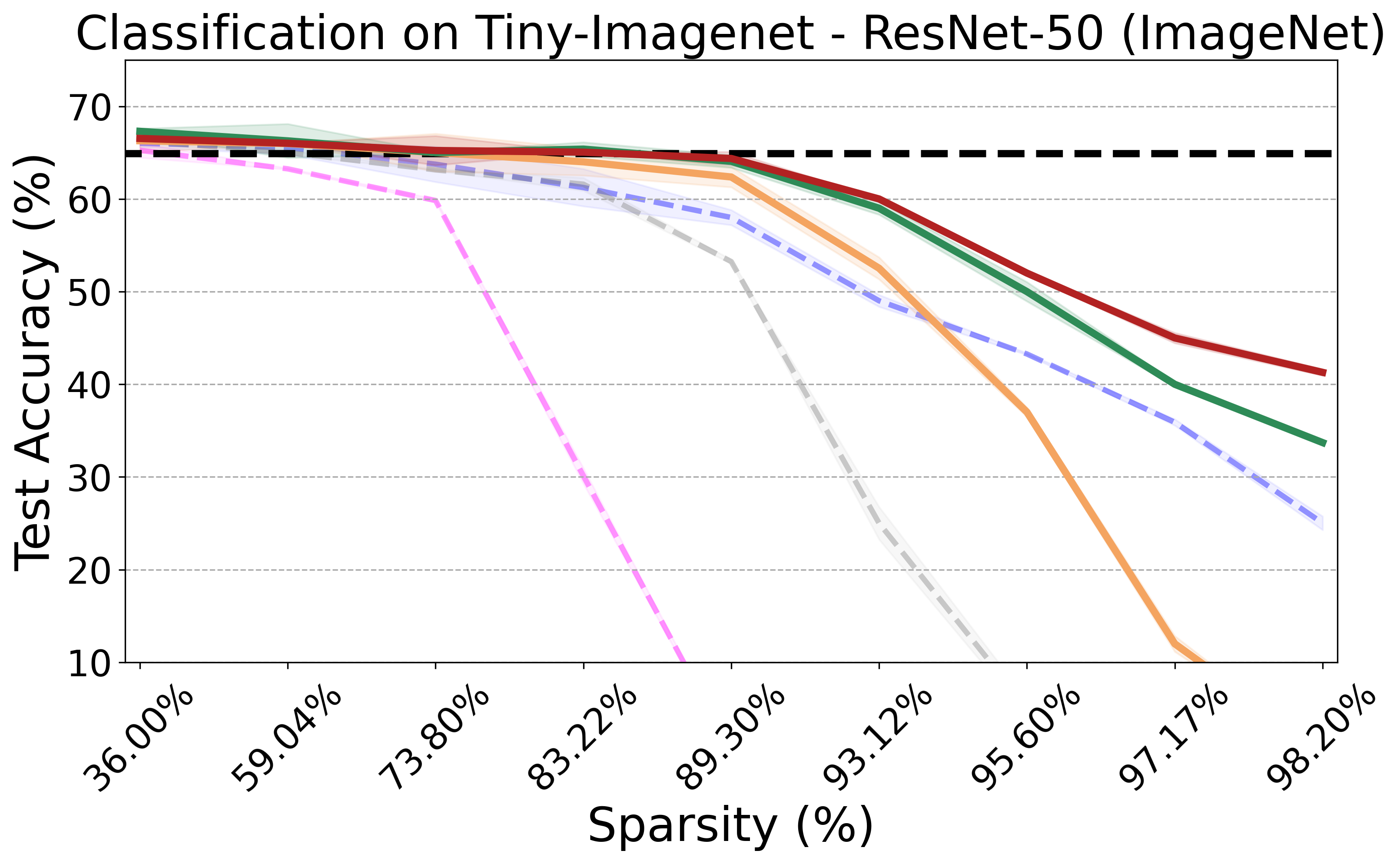
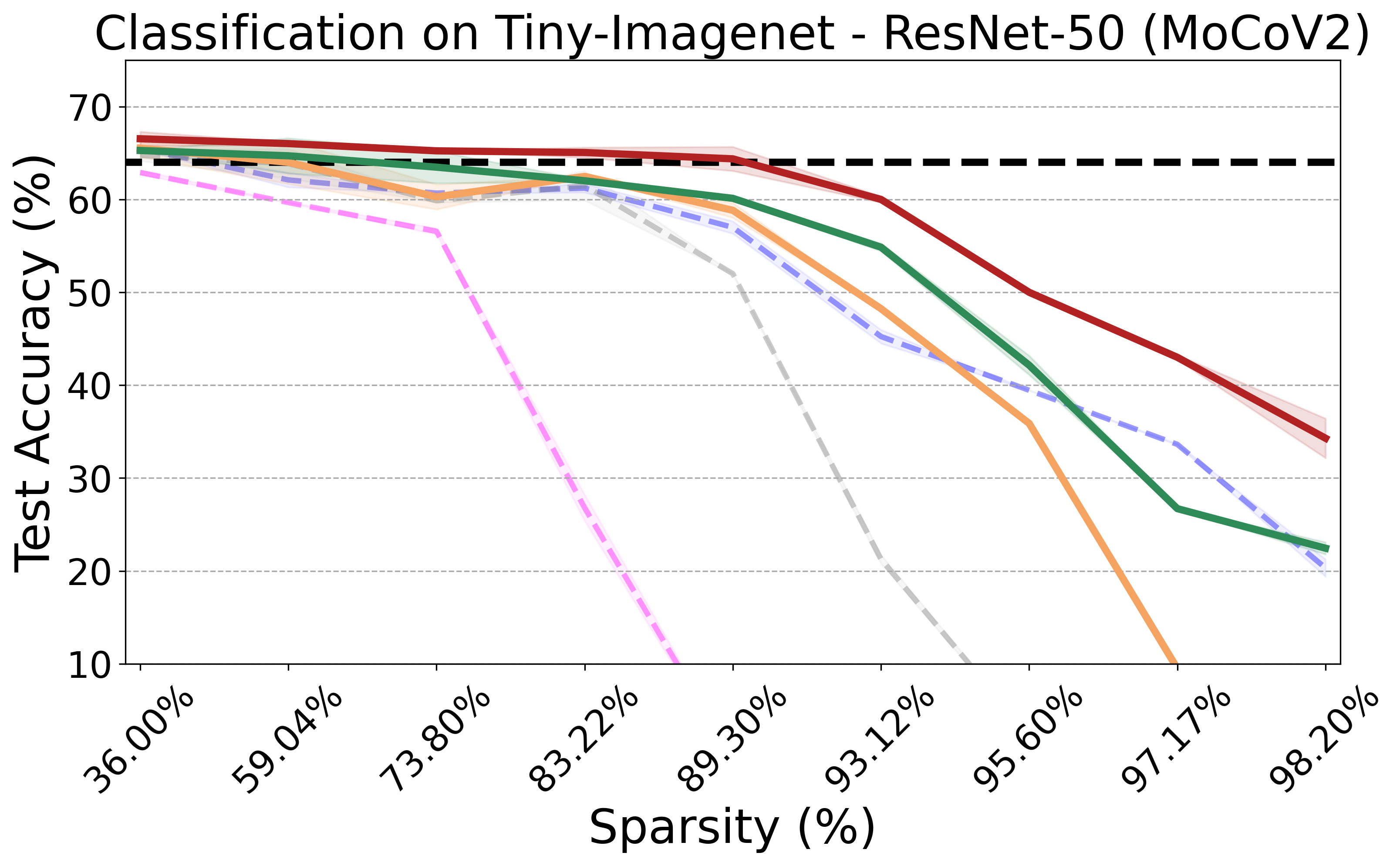
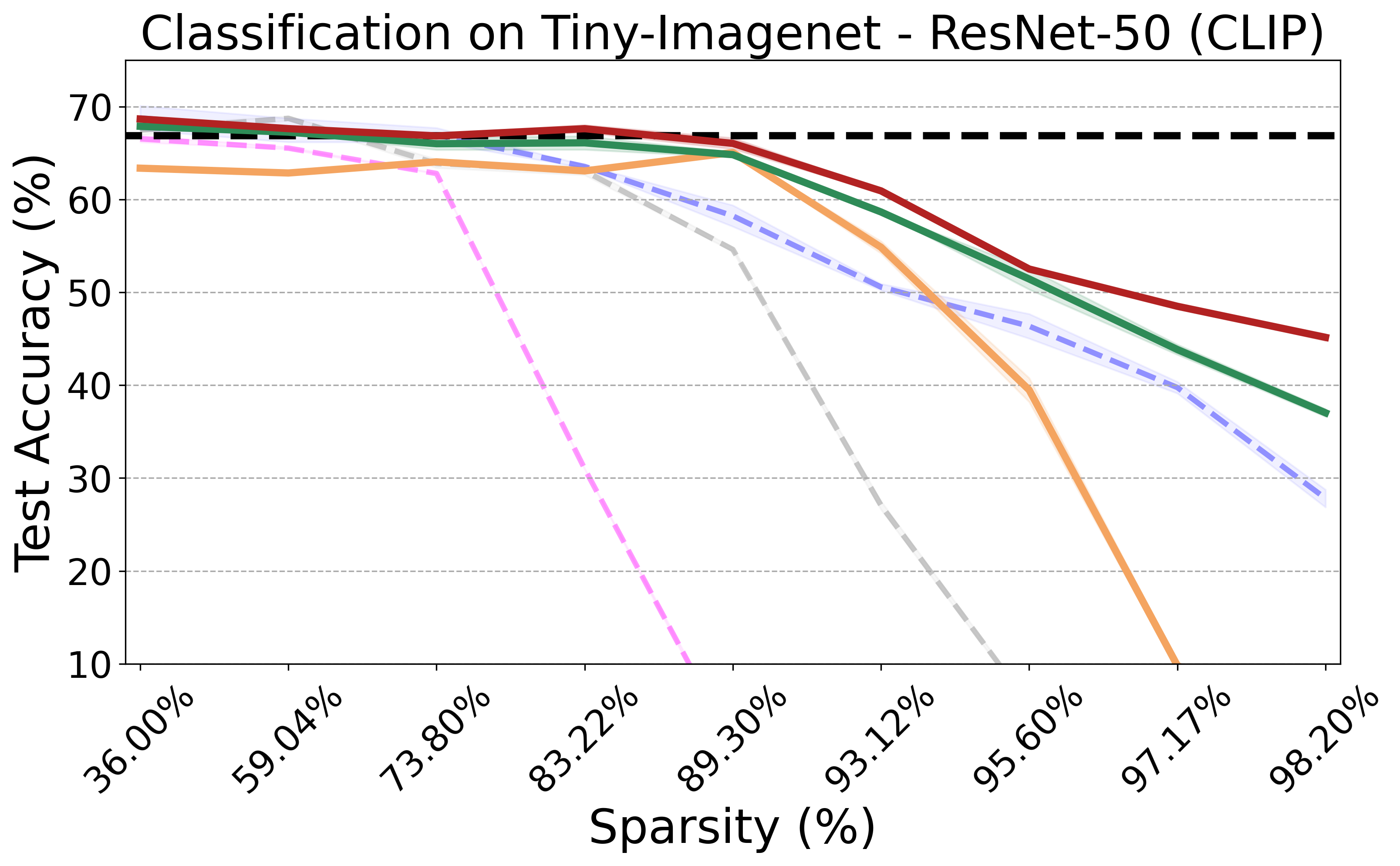
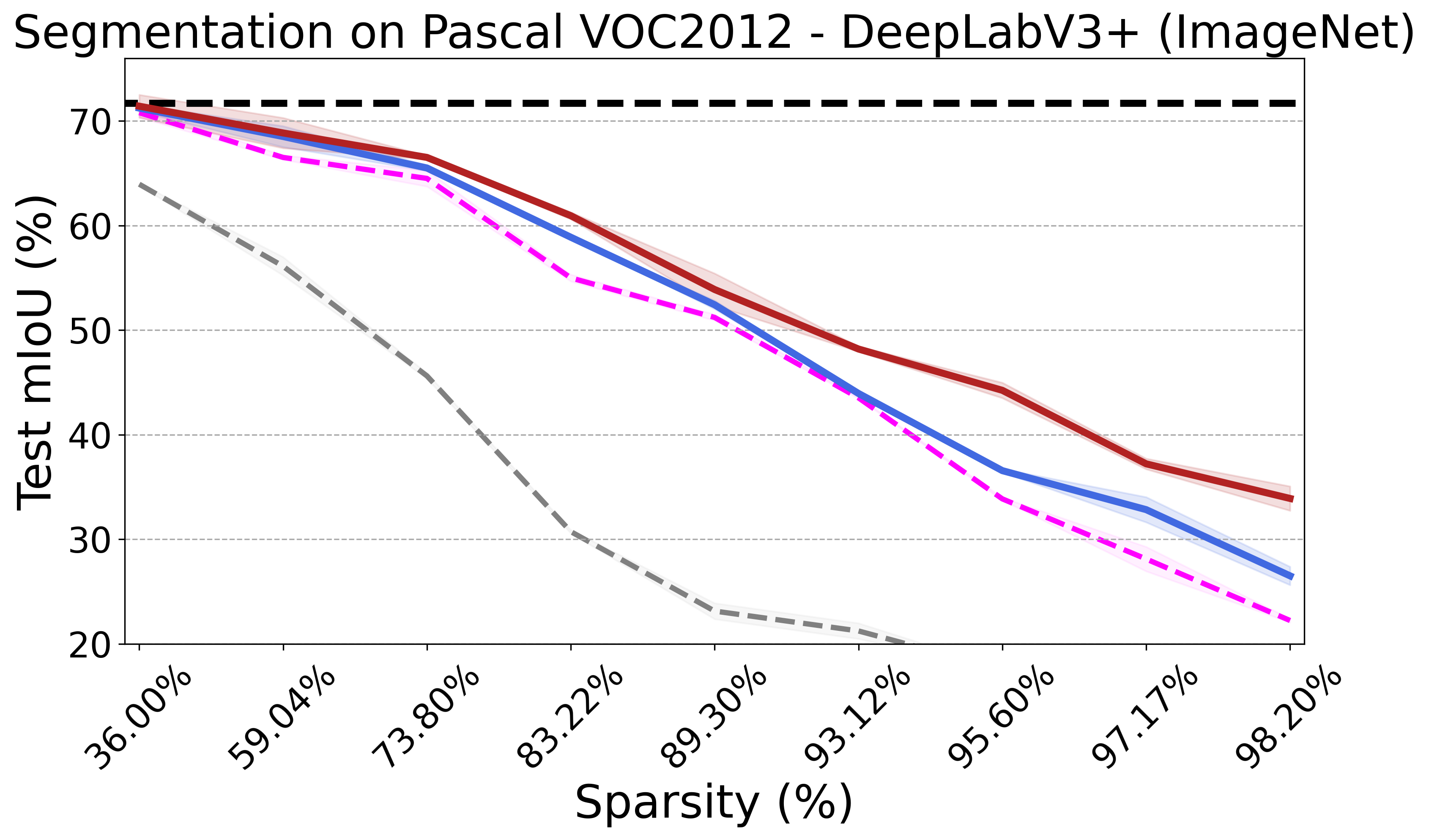
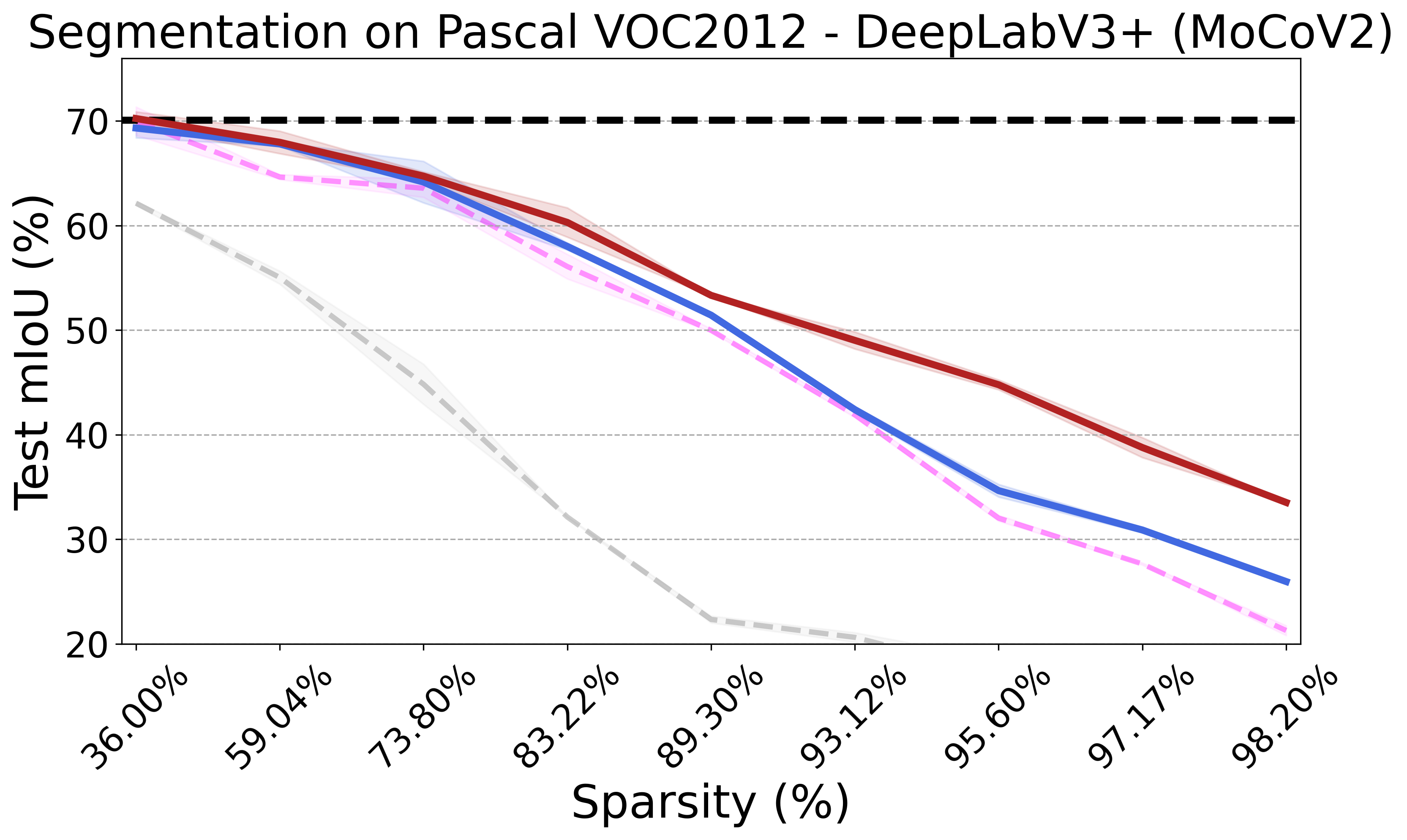
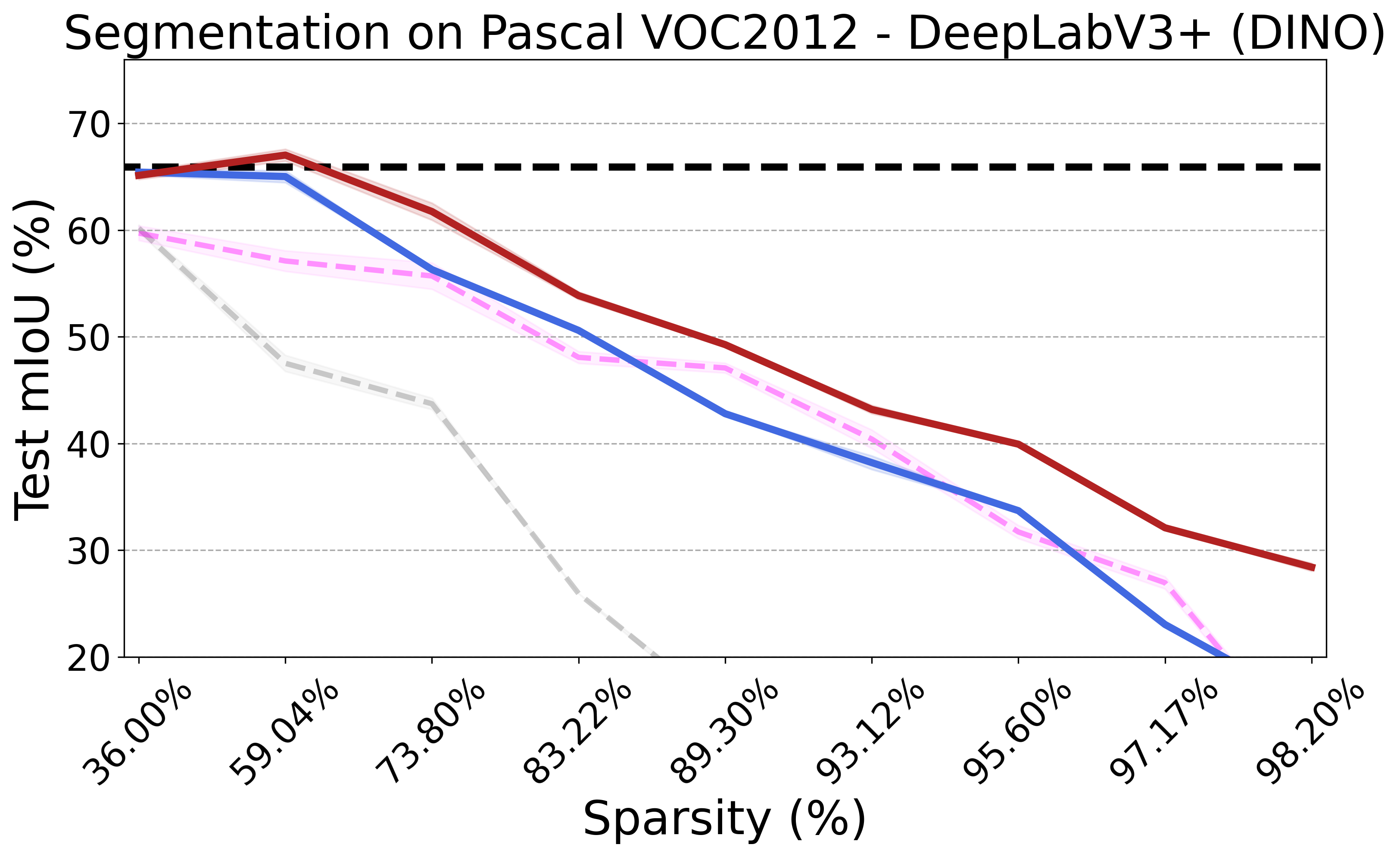
Recent advances in neural network pruning have shown how it is possible to reduce the computational costs and memory demands of deep learning models before training. We focus on this framework and propose a new pruning at initialization algorithm that leverages the Neural Tangent Kernel (NTK) theory to align the training dynamics of the sparse network with that of the dense one. Specifically, we show how the usually neglected data-dependent component in the NTK's spectrum can be taken into account by providing an analytical upper bound to the NTK's trace obtained by decomposing neural networks into individual paths. This leads to our Path eXclusion (PX), a foresight pruning method designed to preserve the parameters that mostly influence the NTK's trace. PX is able to find lottery tickets (i.e. good paths) even at high sparsity levels and largely reduces the need for additional training. When applied to pre-trained models it extracts subnetworks directly usable for several downstream tasks, resulting in performance comparable to those of the dense counterpart but with substantial cost and computational savings.

Method

Our paper introduces a novel pruning algorithm, Path eXclusion (PX), designed to enhance the efficiency of neural networks by pruning at initialization. Leveraging Neural Tangent Kernel (NTK) theory, PX focuses on identifying and retaining the most critical network paths, ensuring minimal performance loss even when the network is transferred to new tasks.

The PX algorithm iteratively prunes network weights that have minimal impact on the NTK trace, thus preserving essential paths and maintaining the training dynamics of the resulting subnetwork aligned with its dense counterpart. Improving on current pruning methods focusing on the NTK theory, our approach leverages a new upper bound for the NTK trace, which takes into account the network's input-output paths based on architecture and weight values (captured by the Path Kernel \(J_\theta^v\)) and how data maps onto such paths (captured by the Path Activation Matrix \(J_v^f(X)\)). Formally, our upper bound is defined as \[\text{Tr}[\Theta(X,X)] = \|\nabla_\theta f(X,\theta)\|_F^2 = \|J_v^f(X) J_\theta^v \|_F^2 \leq \|J_v^f(X)\|_F^2 \cdot \|J_\theta^v \|_F^2, \] which can be efficiently computed using automatic differentiation.

Key Steps in PX Algorithm

NTK Theory and Network Paths. Utilizing NTK theory to express its trace via network paths, providing a robust theoretical foundation for pruning.
Path eXclusion (PX). Pruning weights based on their impact on the NTK trace, ensuring that crucial network paths are retained. The saliency function derived from the NTK trace ensures positive scores for parameters, preventing layer collapse.
Iterative Pruning Process. Gradually refining the mask to focus on the most significant connections, enhancing efficiency and performance.

Main Results

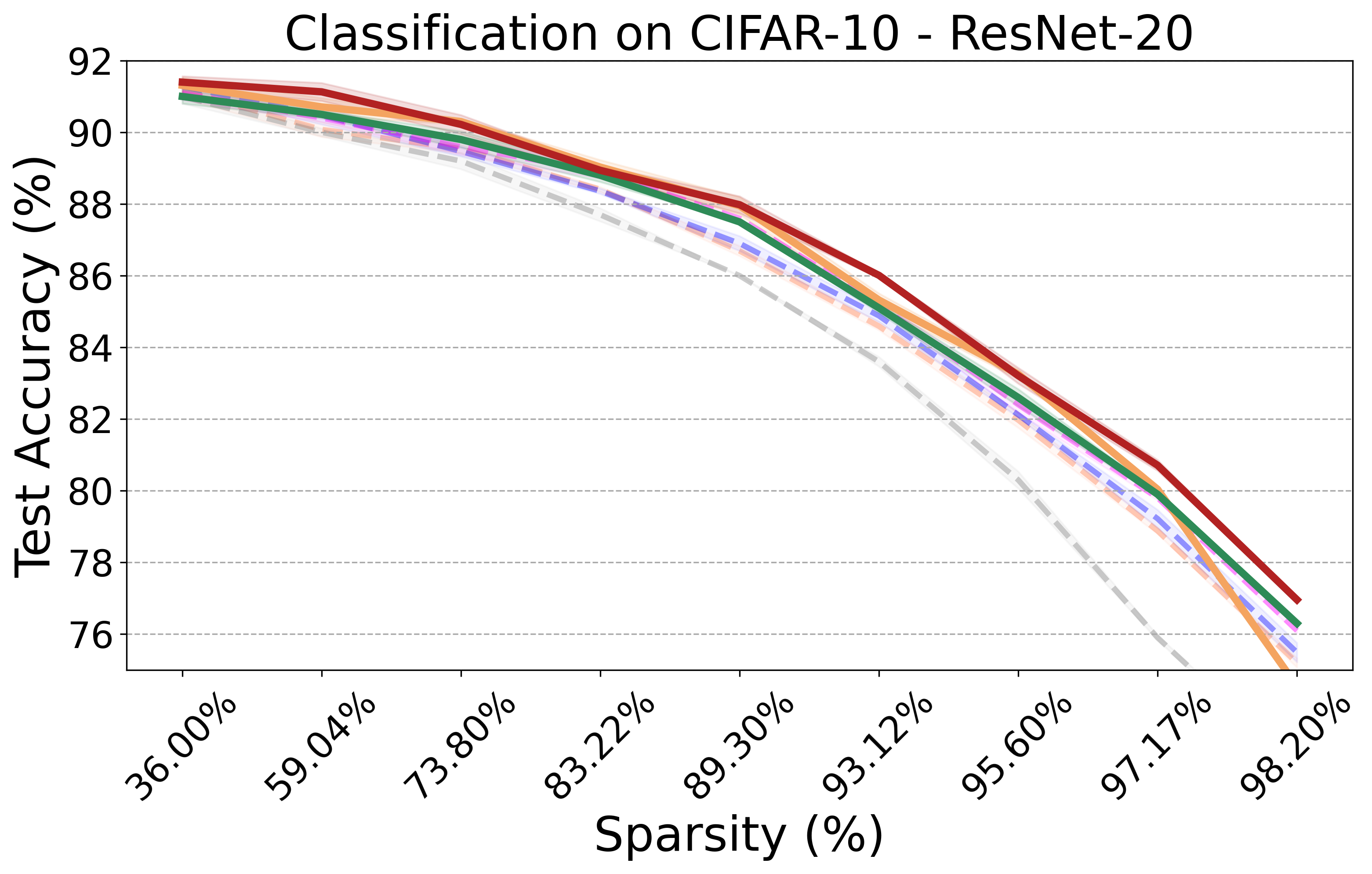
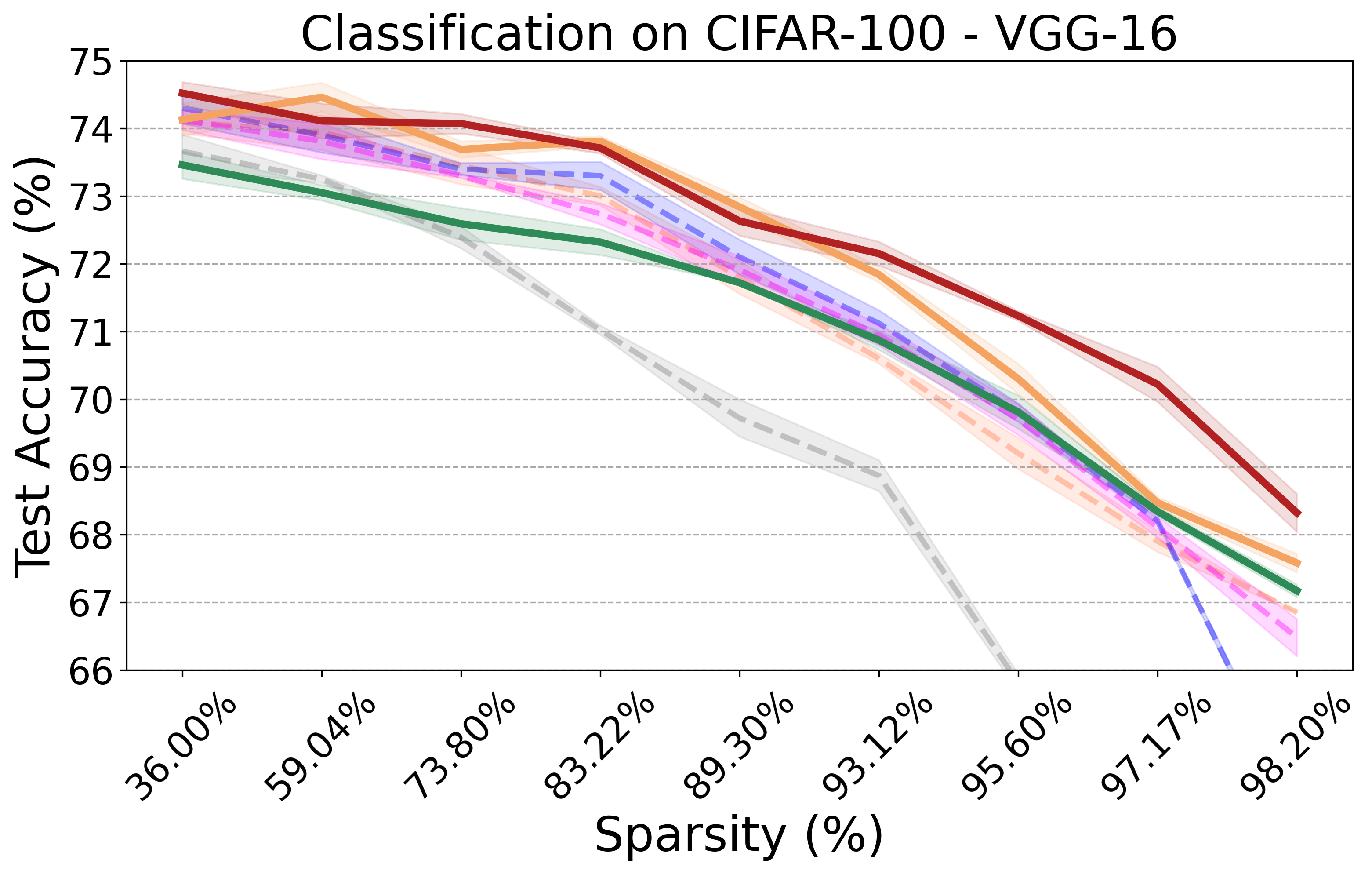
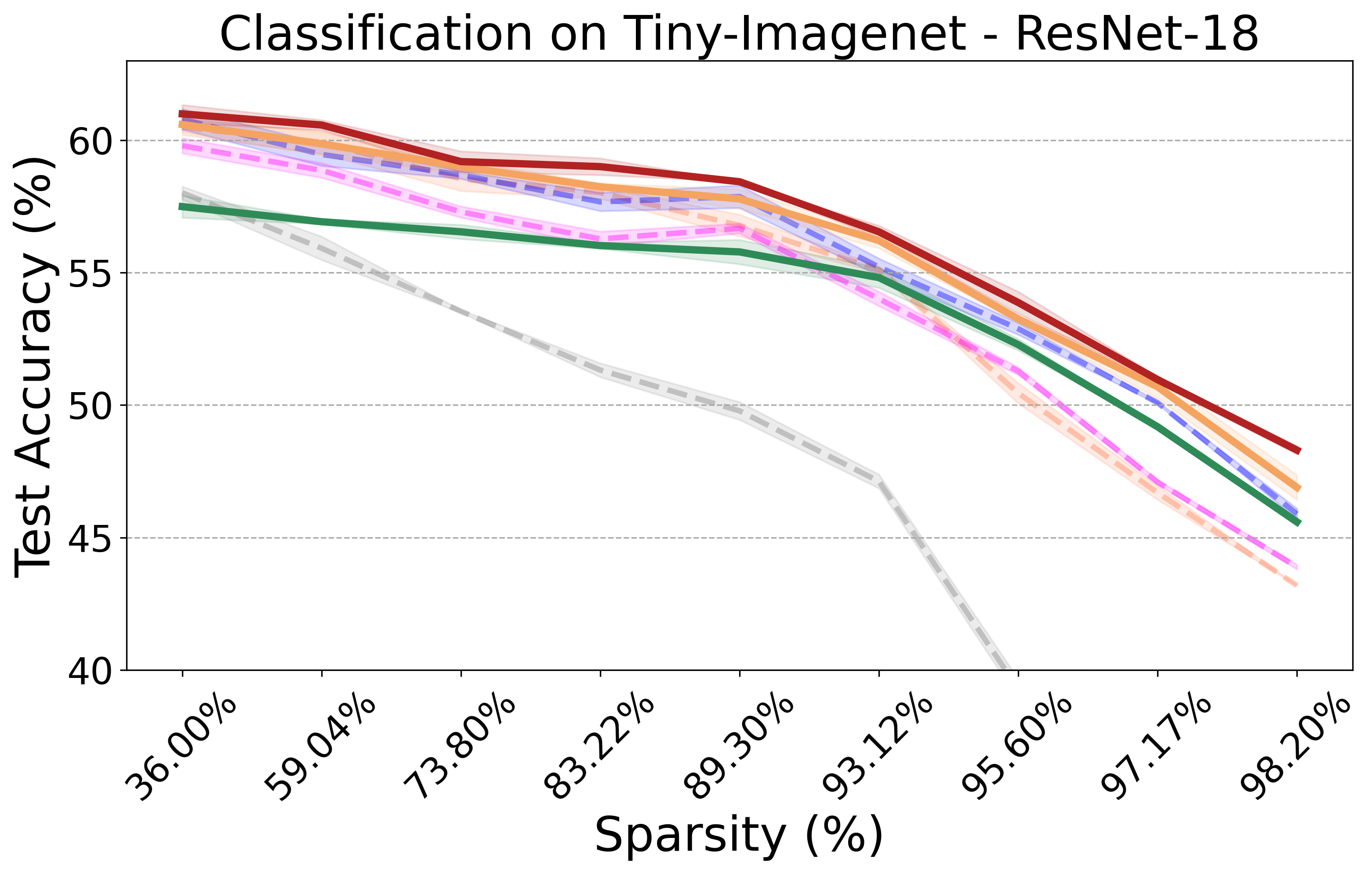
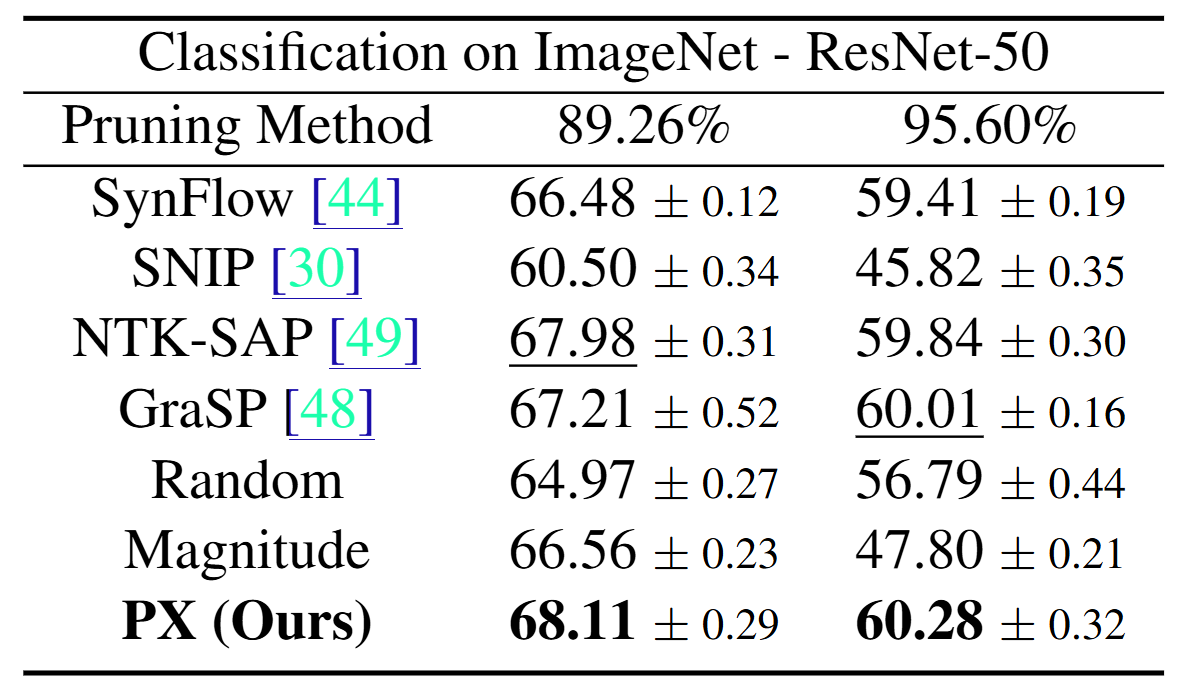
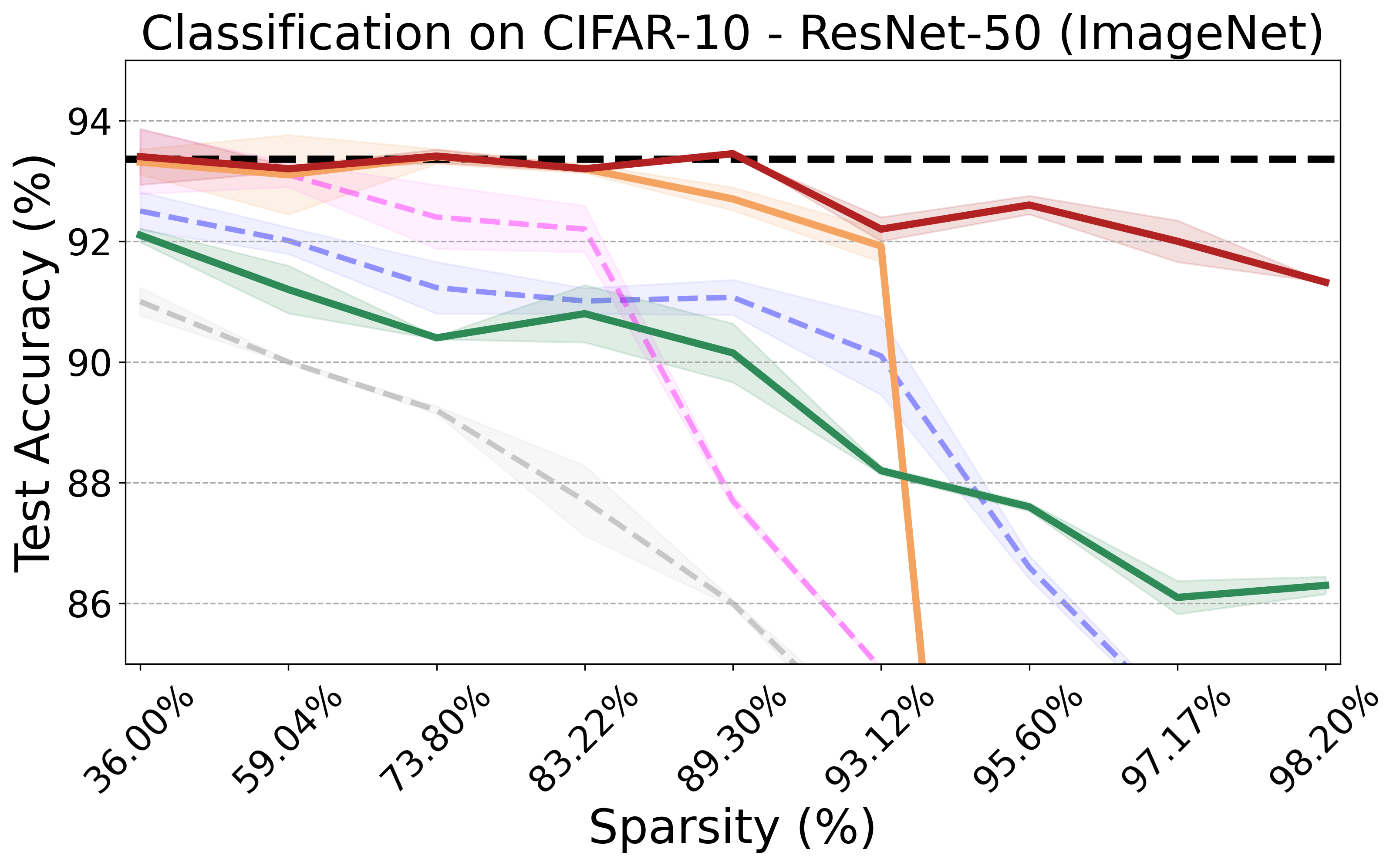
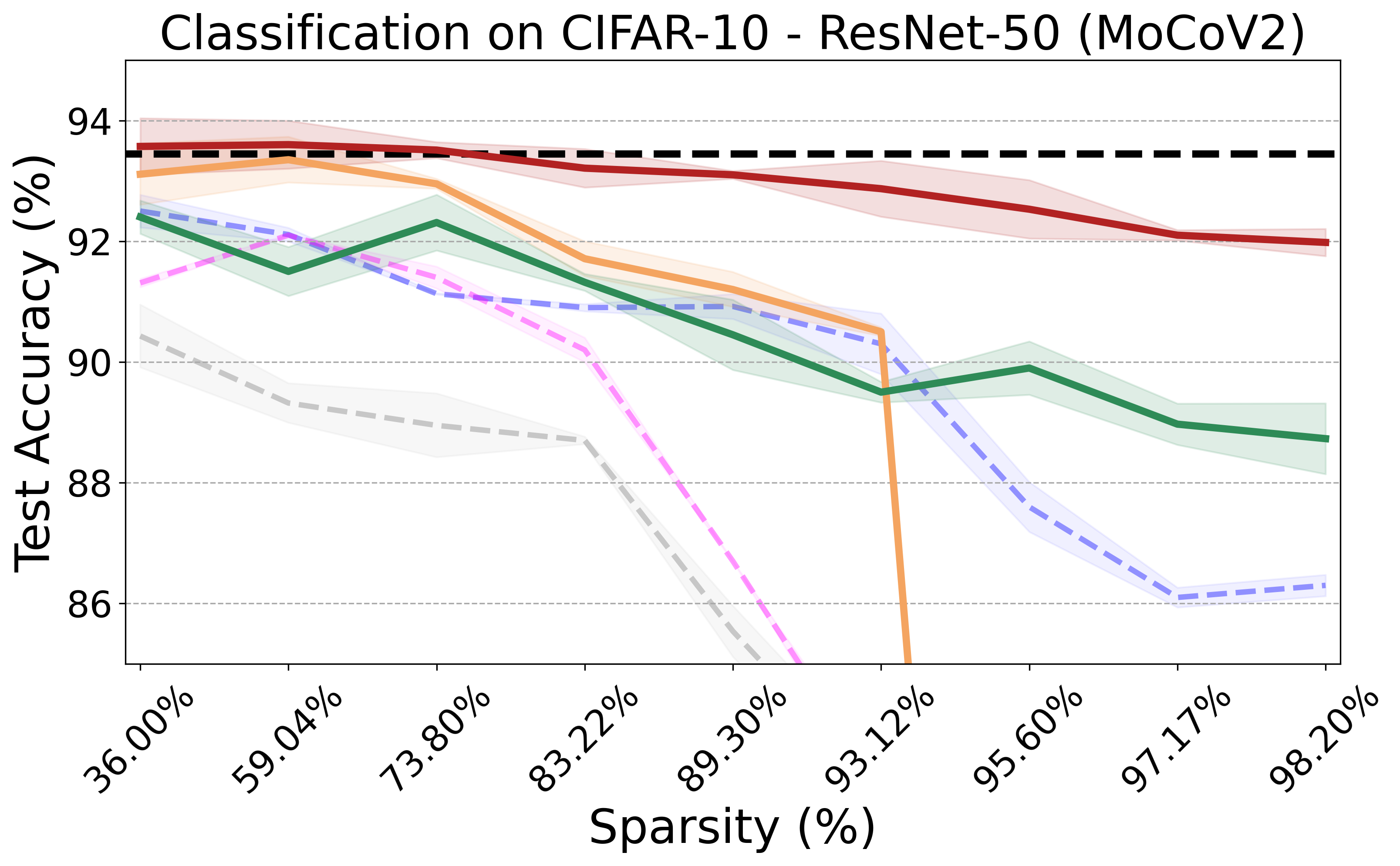
PX demonstrates robust performance across various neural network architectures and tasks, including large pre-trained vision models. It maintains the transferability and effectiveness of pruned networks. The algorithm's theoretical rigor and practical efficiency make it a versatile tool for modern neural network pruning.

Pruning Randomly Initialized Networks

Path eXclusion (PX) on CIFAR10 - ResNet20 Random Init. — Figure 2. Average classification accuracy at different sparsity levels on CIFAR-10 using ResNet-20, CIFAR-100 using VGG-16 and TinyImageNet using ResNet-18, respectively. Each experiment is repeated three times. We report in shaded colors the standard deviation.

Path eXclusion (PX) on CIFAR100 - VGG16 Random Init. — Figure 2. Average classification accuracy at different sparsity levels on CIFAR-10 using ResNet-20, CIFAR-100 using VGG-16 and TinyImageNet using ResNet-18, respectively. Each experiment is repeated three times. We report in shaded colors the standard deviation.

Pruning Pre-trained Models

Path eXclusion (PX) on CIFAR10 - ResNet50 ImageNet pretrain. — Figure 3. Average classification accuracy at different sparsity levels on CIFAR-10, CIFAR-100 and Tiny-ImageNet using pre-trained ResNet-50 as architecture. The first column reports the results of starting from the supervised ImageNet pre-training. The second column reports the performance when starting from the MoCov2 pre-training on ImageNet. Finally, in the third column we report the results when starting from CLIP. Each experiment is repeated three times. We report in shaded colors the standard deviation.

Path eXclusion (PX) on CIFAR10 - ResNet50 MoCoV2 pretrain. — Figure 3. Average classification accuracy at different sparsity levels on CIFAR-10, CIFAR-100 and Tiny-ImageNet using pre-trained ResNet-50 as architecture. The first column reports the results of starting from the supervised ImageNet pre-training. The second column reports the performance when starting from the MoCov2 pre-training on ImageNet. Finally, in the third column we report the results when starting from CLIP. Each experiment is repeated three times. We report in shaded colors the standard deviation.

Pruning Semantic Segmentation Models

Path eXclusion (PX) on Pascal VOC 2012 - ResNet50 DeepLabV3+ ImageNet pretrain. — Figure 4. Average mean Intersection over Union (mIoU) at different sparsity levels on Pascal VOC2012 using DeepLabV3+ with pretrained ResNet-50 as the backbone. Each experiment is repeated three times. Standard deviations are in shaded colors.

Path eXclusion (PX) on Pascal VOC 2012 - ResNet50 DeepLabV3+ MoCoV2 pretrain. — Figure 4. Average mean Intersection over Union (mIoU) at different sparsity levels on Pascal VOC2012 using DeepLabV3+ with pretrained ResNet-50 as the backbone. Each experiment is repeated three times. Standard deviations are in shaded colors.

BibTeX

@inproceedings{iurada2024finding,
  author    = {Iurada, Leonardo and Ciccone, Marco and Tommasi, Tatiana},
  title     = {Finding Lottery Tickets in Vision Models via Data-driven Spectral Foresight Pruning},
  booktitle = {CVPR},
  year      = {2024},
}